渦街流量計基本工作原理
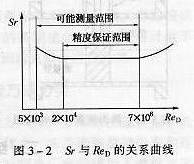
如圖3-1所示,在測量管道中垂直插入一非流線型阻流體,也稱發生體 。隨著流體流動,當管道雷諾數達到一定值時,
在發生體兩側就會交替地分離出卡曼渦街。旋渦頻率f與流經發生體兩側的平均流速U1之間的關系可表示為:
f=SrU1/d
式中:
f--旋渦頻率,Hz;
Sr--斯特勞哈爾系數;
U1--發生體兩側的平均流速,m/s;
d--發生體迎流面的寬度,m.
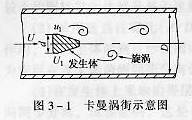
設測量管內徑為D,發生體兩側弓形流通面積之和與測量管的橫截面面積之比為m,則
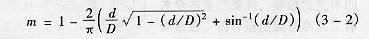
根據流體連續性定理
U1=U/m
式中:
U--測量管內的平均流速,m/s;
根據上兩式可得:
f=SrU/md;
設測量管內瞬時體積流量為qv,則
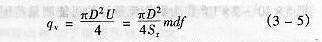
從上式可看出,對于確定的測量管內徑D和發生體迎流面寬度d,流體的狀態體積流量qv與旋渦頻率f成正比。也就是說
,只要測量出旋渦頻率f,就可以測量出體積流量。
對式3-5做一下變換,則:
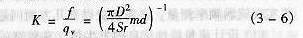
式中
K--渦街流量計的儀表系數,m
-3;
qv--體積流量,m
3/s;
在工程應用渦街流量計測量流量時,常用公式為:
qv=f/K
式中,qv--體積流量,m
3/h.
從上述公式可以看出,用渦街流量計測量流體的體積流量,主要是通過測量旋渦頻率f來實現。而旋渦平率f只與流速U
和發生體的幾何參數(形狀和幾何尺寸)有關,而與被測流體的特性和組分無關。
儀表系數K與以下因素有關:
1.發生體、測量管的幾何尺寸;
2.斯特勞哈爾數Sr,斯特勞哈爾數又與發生體的形狀和雷諾數有關。圖3-2是已商品化的渦街流量計的Sr與Re
D的關系曲
線。對于多數渦街流量計,管道雷諾數Re
D在2*10
4~7*10
6范圍內,斯特勞哈爾數Sr可視為常數,可保證測量的精度。超
出該范圍,Sr將隨Re
D的降低或升高而變化,渦街流量計將出現非線性。當ReD從2*10
4降低到5*10
3時,卡曼渦街仍可穩
定分離。但由于非線性的影響,測量精度會降低。所以,抱5*10
3~7*10
6作為渦街流量計的可能測量范圍。